Understanding the Cost of a Decision Threshold

The decision threshold is what determines the point above which are classifier's prediction is considered positive and below which it is considered negative. As such, how many positive classification and negative classification decisions are made is dependent on the chosen decision threshold.

Furthermore, this has an impact on how many false positives or false negatives we end up with. If the decision threshold is very high, then very few examples will be classified as positive in the first place, in relative terms. Fewer total positive predictions means fewer false positive predictions and precision goes up while recall goes down.

In the same way, if the decision threshold is very low, then very few predictions will be negative in relative terms. Fewer total negative predictions means fewer false negatives and recall goes up while precision goes down.

But how do we decide what the ideal decision threshold should be? The answer depends entirely on the context and business use case. For some applications, false positives are more expensive while in others, false negatives are more expensive where expense is measured in some way.

We will consider the equation below to measure our total expense where w_i is the weight determing the cost of a classifier's decision.

\[ Total \space Cost = w_{FN} * False \space Negatives + w_{FP} * False \space Positives + w_{TP} * True \space Positives + w_{TN} * True \space Negatives. \]

For our example, for simplicity, we will assume that false negatives are ten times more expensive than false positives and true positives while true negatives have no cost. A scenario where this assumption is suitable, may be customer churn prediction. We will capture this in the equation below.

\[ Total \space Cost = 10 * False \space Negatives + 1 * False \space Positives + 1 * True \space Positives + 0 * True \space Negatives. \]

Considering this equation as our cost, we will plot the cost as a function of the decision threshold.

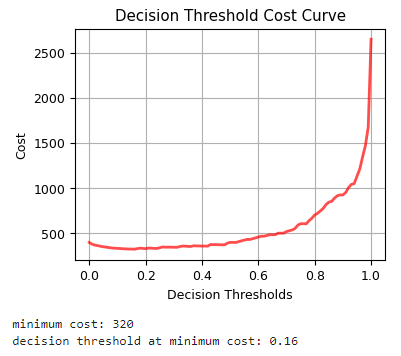
We see that our optimal decision threshold is at 0.16. We will plot our metrics at this threshold.

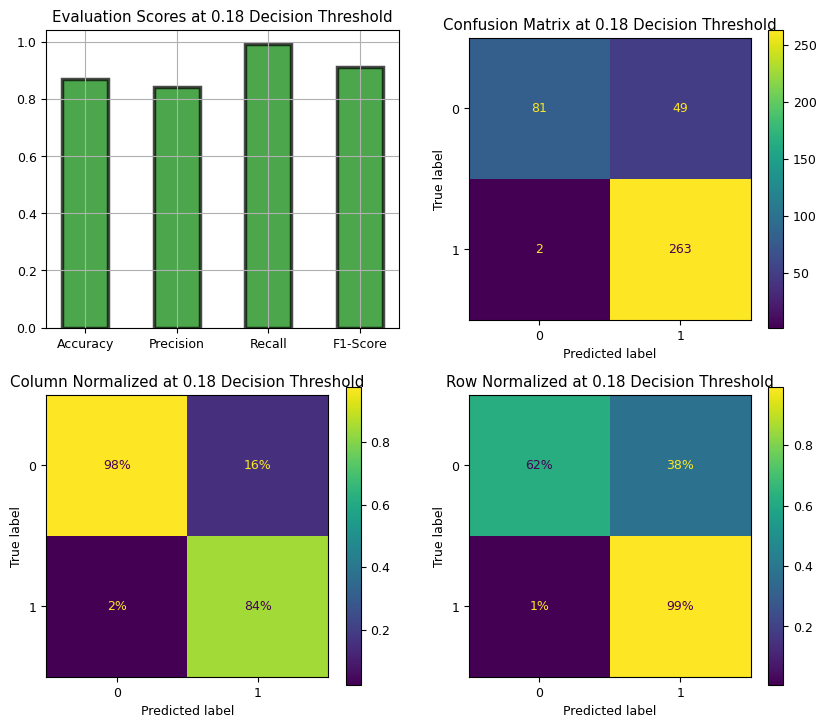
We see that false negatives sink, recall goes up to almost 100% while precision drops significantly.